不同于线性表的一对一和树型结构的一对多的简单结构,图结构是一种元素多对多的复杂结构。
这里主要介绍:
- 图的各种定义
- 图的顶点与边之间的关系
- 图的存储结构(邻接矩阵、邻接列表等)
- 图的遍历方法(深度优先、广度优先)
- 最小生成树算法(Prim 算法、Kruskal 算法)
# 图的各种定义
- G (V,E):V 为顶点的集合,E 为边的集合
- 无向边:顶点 Vi 到 Vj 之间的边没有方向,用无序偶(Vi,Vj)来表示,(Vi,Vj) 与 (Vj,Vi) 一个意思
- 有向边:也称为弧,用有序偶<Vi,Vj>来表示,Vi 为弧尾,Vj 为弧头
- 无向完全图:无向图中,任意两个顶点之间都存在边。含有 n 个顶点的无向完全图有 条边。
- 有向完全图:有向图中,任意两个顶点之间都存在方向互为相反的两条弧。含有 n 个顶点的有向完全图有 条边。
- 稀疏图和稠密图:边或弧数以 为分界。
- 网:即带权的图。
- 子图:假设 G1=(V1,E1),G2=(V2,E2),V2V1 并且 E2E1,则 G2 为 G1 的子图。
# 图的顶点与边之间的关系
对于无向图:
- 邻接点:G=(V,E),(V1,V2)E,则 V1 和 V2 互为邻接点。(V1,V2) 依附于 V1 和 V2,(V1,V2) 与 V1 和 V2 相关联。
对于有向图:- 邻接:G=(V,E),<V1,V2>E,则 V1 邻接到 V2,V2 邻接自 V1。
- ID (V):V 的入度(箭头指向 V 的数目)。
- OD (V):V 的出度(从 V 指出去的箭头数)。
- TD (V):和 V 相关联的边的数目。[TD(V)=ID(V)+OD(V)]
- 路径:从 V1 到 V2 能走的路。
- 路径的长度:路径上的边或弧的数目。
- 环 (回路):第一个顶点到最后一个顶点相同的路径。
- 简单环:除首尾顶点(相同的一个顶点)外其余顶点不重复出现的环。
- 连通:V1 到 V2 有路径,则 V1 和 V2 是连通的。
- 连通图 / 强连通图:图中任意顶点 Vi 和 Vj 都是连通的。(有向图符合 -> 强)
- 连通分量 / 强连通分量:无向图中的极大 连通子图。(同上)
- 连通图的生成树:即一个极小的连通子图,含有图中全部的 n 个顶点,但只有 n-1 条边(对一个图删去多余的边)。
- 有向树:恰有一个顶点的入度为 0,其余顶点的入度均为 1 的有向图。
# 图的存储结构
下面使用
C语言来描述数据结构
先把最小单位定义一下:
typedef char[4] Vertex;// 顶点信息 | |
typedef int Weight;// 权重 | |
typedef int Number;// 数值类 |
# 邻接矩阵
typedef Weight** Matrix;// 矩阵 | |
typedef struct GMatrix {// 邻接矩阵存储结构 | |
Vertex* data;// 一维数组存放顶点信息 | |
Number n;// 顶点数 | |
Matrix M;// 二维数组 | |
}; |
# 邻接列表
- 这种存储结构对于
边数相对顶点较少的图可以极大程度的节省存储空间,避免浪费
typedef struct UGLBox {// 无权邻接表项 | |
Number v;//Vertex 顶点索引 | |
UGLBox* next;// 指向下一无权表项 | |
}; | |
typedef struct WGLBox {// 有权邻接表项 | |
Number v;//Vertex 顶点索引 | |
Weight w; | |
WGLBox* next;// 指向下一有权表项 | |
}; | |
typedef struct GLHead {// 邻接列表头 | |
Vertex data;// 顶点名称 | |
void* B;//Box 表项 | |
}; | |
typedef struct GList {// 邻接列表存储结构 | |
Number len;// 表长 | |
GLHead* Head;// 指向表头数组 | |
}; |
针对有向图还可以改进为十字链表
typedef struct GOBox {// 十字链表项 | |
Number tailV; | |
Number headV; | |
GOBox* tail; | |
GOBox* head; | |
}; | |
typedef struct GOHead {// 十字链表头 | |
Vertex data; | |
GOBox* tail; | |
GOBox* head; | |
}; | |
typedef struct GOList {// 十字链表存储结构 | |
Number len; | |
GOHead* Head; | |
}; |
同样的,针对无向图也可以改进为邻接多重表,减少增减表项时的开支
typedef struct GMBox { | |
Number tailV; | |
GMBox* tail; | |
Number headV; | |
GMBox* head; | |
}; | |
typedef struct GMHead { | |
Vertex data; | |
GMBox* first; | |
}; | |
typedef struct GMList { | |
Number len; | |
GMHead* Head; | |
}; |
# 边集数组
typedef struct Edge { | |
Number begin; | |
Number end; | |
Weight w; | |
}; | |
typedef struct Edges { | |
Number len; | |
Vertex* v; | |
Edge* e; | |
}; |
最后还可以把输入数据规范化
typedef struct UEdge {// 无权边 | |
Number t;//tailVertex | |
Number h;//headVertex | |
}; | |
typedef struct WEdge {// 有权边 | |
Number t;//tailVertex | |
Number h;//headVertex | |
Weight w; | |
}; | |
typedef struct GInput {// 图输入 | |
Vertex* data;// 顶点 | |
Number n;// 顶点数 | |
void* Edges;// 边的关系 | |
Number len;// 边的关系的数量 | |
}; |
# 图的遍历方法
# 深度优先遍历
按照右手原则,每次选择上一顶点的最右边的下一顶点,走过一个顶点标记一个顶点,不能走被标记过的顶点,一条路走到黑,直到无路可走,然后回溯。
这个就是先走到最大深度,不能再深入后,再返回到有支路可走的顶点继续深入到最下面。
- 总结:层层递归,碰壁回溯。(或是使用栈:出栈入栈,依次访问。)
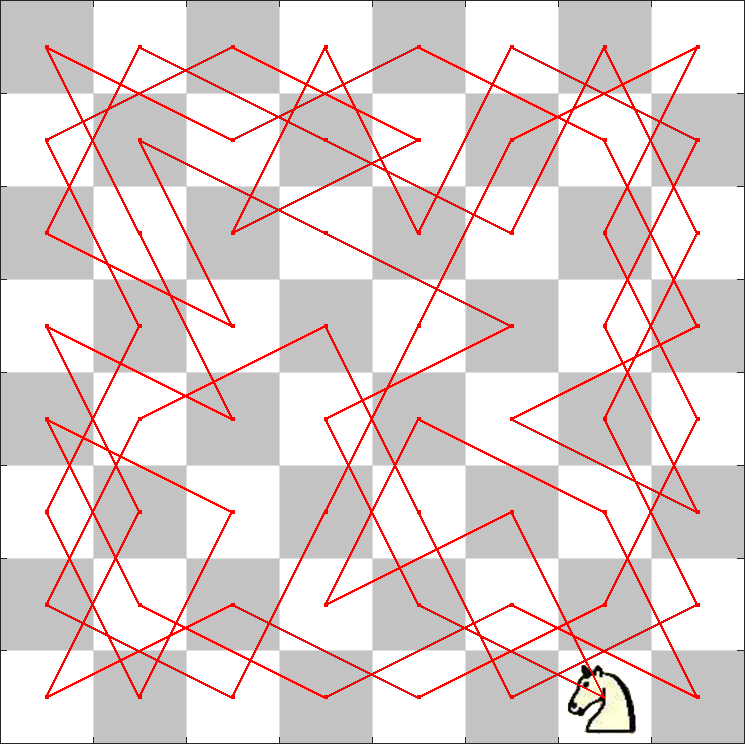
# Example: 马踏棋盘算法
马踏棋盘算法,也称骑士周游问题。在一个 8x8 的国际象棋棋盘上,用一个马按照马步(即走日字,同中国象棋的马的走法)跳遍整个棋盘,要求每个格子都只跳一次,最后回到出发点。
问题分析
- 棋盘的表示(二维数组)
- 计算马的下一步可能的位置
关于马的走法:
通过对位移参数 1 和 2,y 轴对称,y=x 对称,y=-x 对称三步可以列出所有可能的下一步位置。(或者直接手写 8 个坐标偏移)- 判断可能的位置是否合法(没有超出边界且该位置还没有被遍历过)
- 递归,回溯,直到找出解
这一步还可以用贪心算法优化:
我们要走的下一步位置,它的可选下一步位置数(记为权重)应当最少;
对下一步位置的权重集合进行非递减排序(可以有重复值的递增排序);
然后按照这个排序结果遍历,就可以少很多次递归。代码
马踏棋盘算法.cpp >folded
#include <stdio.h>#include <stdlib.h>#include <math.h>#define X 8#define Y 8// 定义两个数据结构,分别用来存放坐标信息和权值信息// 下一个可能跳的坐标xybox xy;}// 建立马跳的格子的增量数据,总共 8 种情况 返回指针指向 xybox [8]//y=x 镜像处理}//y=-x 镜像处理}}// 遍历棋盘,深度优先,使用贪心算法优化// 找到解,输出}}}xybox xy;weightbox weight;// 超出边界或已被遍历,下次循环}// 否则标记,并继续递归xybox xytmp;// 模拟下一次遍历,并将遍历后可走格子数记为权重存入权重数组// 超出边界或已被遍历,下次循环}}}}}// 遍历失败,回溯}// 按权值从小到大排序}}// 依次遍历(贪心算法)}}// 遍历失败,回溯}}// 这边数组输入 X 和 Y 是反过来的 chess [Y][X]}}
# 广度优先遍历
利用队列,每次把上一顶点的所有可选下一顶点依次排入队列,然后按照这个队列依次访问,类似树的层级遍历。
这个就像是每深入一层,就把这一深度下的所有顶点都先访问一遍,再往下深入。
- 总结:出队入队,依次访问。
# 最小生成树算法
最小生成树:将一个有权连通图转变为树,并且要求生成树的权值总和要最小。
# 普里姆算法
普里姆算法从顶点入手寻找最佳路线,对于稠密图有优势,遵循以下规则:
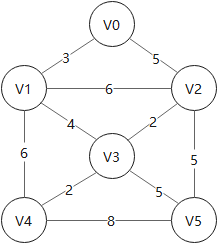
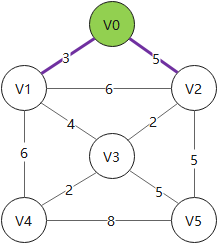
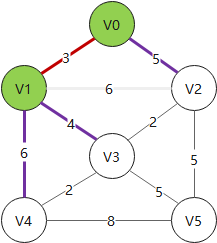
- 1. 将遍历过的顶点涂为
绿色 - 2. 将遍历过的顶点(
绿色顶点)的相关边涂为紫色 - 3. 若一个未被遍历过的顶点(
白色顶点)与多条紫色边相连,则只保留权值最小的紫色边,其余紫色边弃掉 - 4. 将
紫色边中权值最小的那条涂为红色,与其相连的顶点连入生成树 - 5. 在保证 1、2、3 的情况下重复步骤 4
Example:
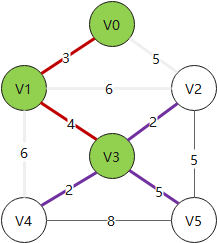
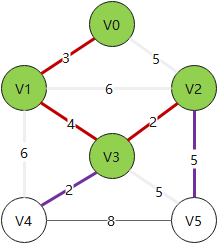
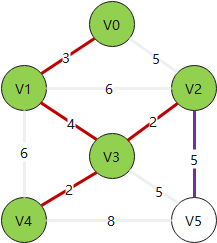
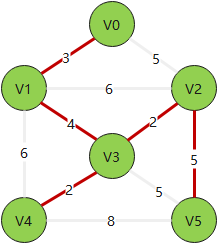
# 克鲁斯卡尔算法
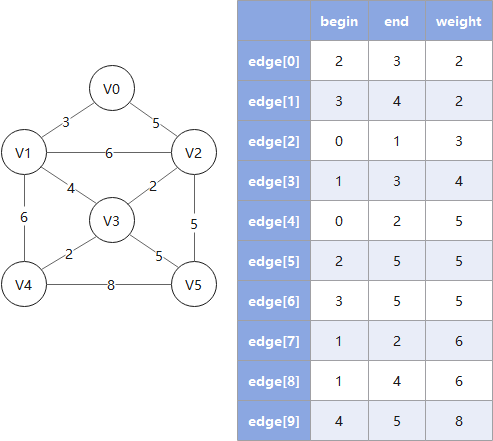
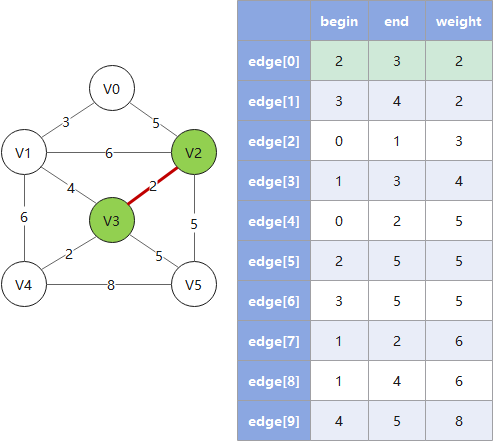
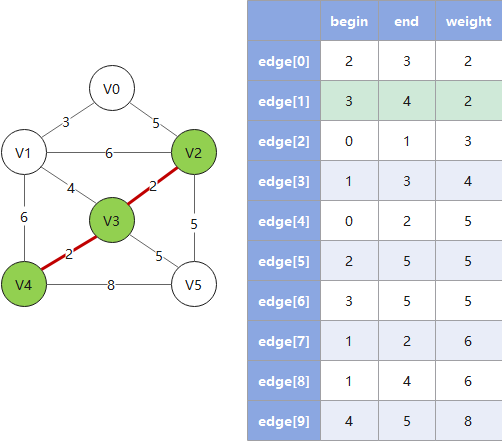
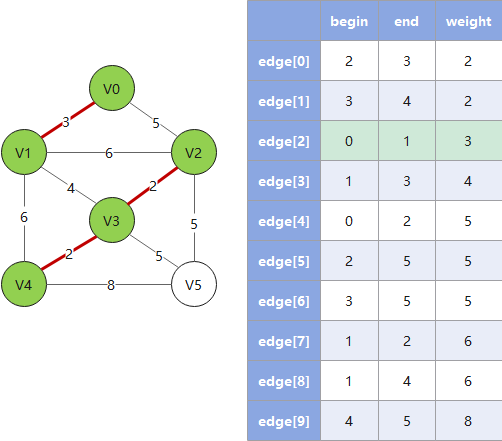
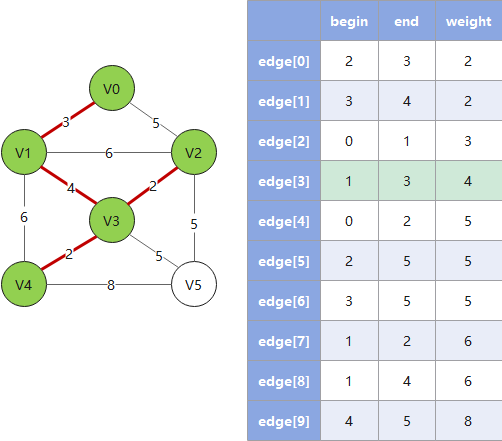
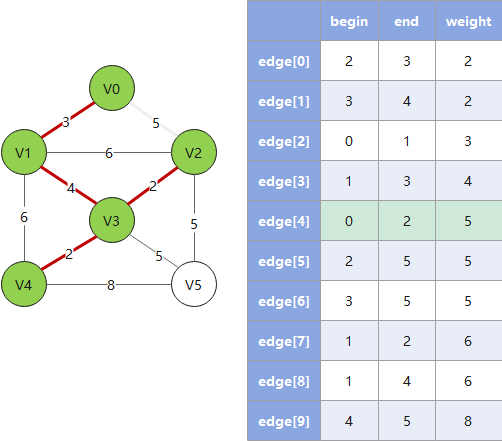
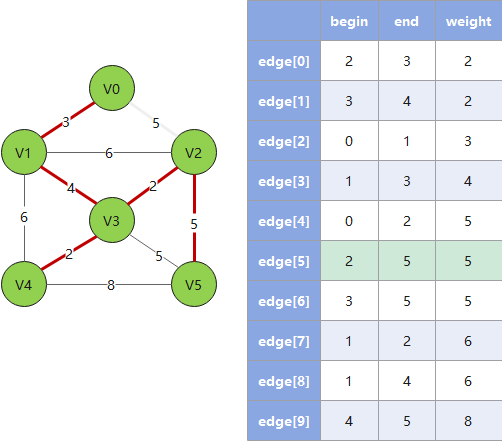
克鲁斯卡尔算法从边入手寻找最佳路线,对于稀疏图有优势,遵循以下规则:
- 1. 按权值大小对边进行非递减排序
- 2. 依次将边接入生成树,并把树信息存入
parent数组(这里 parent 数组的算法是一个关键) - 3. 检查下一个接入的边是否会和已有边构成环(回路),若构成则跳过这条边(这里用 parent 数组做检查)
- 4. 重复 2、3,直到遍历完所有的边,此时已形成最小生成树
Example:
参考:
C 语言数据结构与算法视频教程全集
VisuAlgo - 图形据结构(邻接矩阵,邻接列表,边缘列表)